The posts here are from January 2009 and can be found in this topic: http://www.speedsolving.com/forum/showthread.php?8628
This is a topic on puzzle theory - specifically, it deals with the theory of symmetrical twisty puzzles. There's no real "theory" section in this forum but it doesn't belong in Off-Topic, so I've put it here so more people will see it. (This does have applications to speedcubing, in terms of solving gelatinbrain puzzles.)
So, as some of you may know, symmetrical twisty puzzles can be described by talking about the shape and the number of separate types of turns in each of the three basic categories (face turns, edge turns, and vertex turns) which are named around where the axis (which the pieces rotate around) points. A 3x3x3, for instance, is a cube with one type of turn (in the face turn category); in my categorization scheme that would make it type Cf (C for cube, f for face turn). The only other type-Cf puzzle is the 2x2x2, which has a deeper turn that just happens to line up with the turn on the opposite face. (The 4x4x4 and 5x5x5 have two face turn types, so they are type Cff. Similarly the 6x6x6 and 7x7x7 are type Cfff.) Note that I'm considering a 3x3 with slightly shallower or deeper cuts to be the same, because it has the same number and types of pieces and the exact same solution, so the only difference is in the shape of the pieces.
If we want to talk about symmetrical puzzles with only one type of turn, it's relatively simple, because we can describe the depth of the turn as a single number. But if we have two types of turns, we need two numbers: for instance, on a 5x5x5, if we imagine a turn of depth 0 to turn nothing and a turn of depth 1 to turn the entire cube, the two turns have depths 1/5 and 2/5. But it's hard to imagine exactly what numbers will give a certain puzzle, and which numbers will give a different one. So the question is this: how many possible puzzles are there of a given type, and, more importantly, how can we understand where one puzzle begins and another ends?
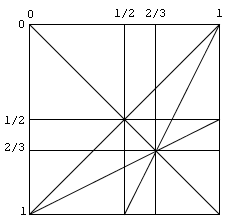
My answer to this is the 2D State Diagram. This particular one describes the Tvv-type polyhedra (that is, tetrahedra with two vertex turn types - note that a vertex turn and a face turn are the same thing on a tetrahedron). The two axes correspond to the two depths of turn, and each one goes from 0 (no part of the puzzle is turned) to 1 (the entire puzzle is turned).
So what are the lines in the diagram? Each one represents some kind of puzzle which only exists for a very specific set of turn depths. The diagonal line from the top-left to bottom-right represents the degenerate case where the two depths are the same (so, type Tv puzzles with only one type of cut). Each of those big spaces between the lines, however, is a specific puzzle, which remains the same anywhere in that space. There are also puzzles on the lines themselves, and each place where lines intersect is another puzzle, albeit a very specific one because even a small change in either of the two depths will make it different. The Pyraminx, for example, is located at the intersection of a horizontal or vertical 2/3 line, and the diagonal line from bottom left to top right.
Finally, I have prepared an interactive simulation (!) of this state diagram, so that you can play with it to see how it works out. It uses the GeoGebra geometry program, which I'm really fond of. You can download it from my website. To use it, just move the red point around inside the square (use the white pointer symbol to move a point around), and watch how the puzzle changes when you cross or move along lines.
I wrote up the state diagram for type Dff puzzles (dodecahedra with two different depths of face turns). The Gigaminx is from this category. Note that this category is MUCH more complicated than the Tvv type I showed in the first post - I'm not completely sure of the count, but I think there are a whopping 98 puzzles of this type!!! I'm really glad I made an interactive simulation, because there is no way I'd ever want to draw all of them out by hand. You can also see that there are 7 puzzles along the diagonal (these are the Df type puzzles).
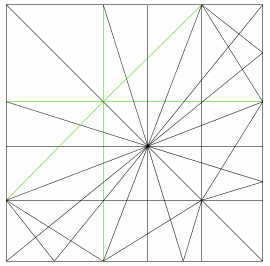
In the image, I have marked a few lines as green. Those lines are distinctive because, although they separate different puzzles, the puzzles on the lines themselves are equivalent to one of the puzzles on one side of the line. For instance the Megaminx and Supernova, although they look like they might different puzzles, function exactly the same way.The full way to count the number of puzzles is:
- Any open space is a separate puzzle, although you have to make sure to only count puzzles on one side of the main diagonal (for everything here).
- Any line segment (i.e. a line between two intersections) is a separate puzzle, except (i) if the line segment is green; (ii) if the line segment is on the main diagonal; (iii) if the line segment is on the top or left. The second and third cases remove puzzles with essentially only one depth of turn, and the first removes a puzzle that looks like a different puzzle but isn't.
- Any intersection of lines is a separate puzzle, as long as (i) it isn't on the the top or left or the main diagonal, and (ii) it has at least two black lines crossing it.
The Tvv case gives 11+10+2 = 23 puzzles like this (I think). Note that, although I haven't added it in yet, the halfway lines and the bottom-left-to-top-right diagonal in the Tvv diagram should also be green. It's only important to know what lines are green and what are not when you are counting puzzles, though.
Finally, there is a GeoGebra simulation of this, although I have made the two-dimensional slider much larger to compensate for the complexity. That way you can really see what lines you are crossing.
For each polyhedron there are actually six types of second-order puzzles: the familiar vv, ee, and ff, but also fv, ev, and ef. The first three use only one type of cut, so they're symmetrical, but the other three use two different types of cuts and have much more complicated drawings. As an example I've made one for the Cfv group. There are around 50 puzzles in this group, most of which have probably never been seen before. I hope to eventually make an interactive simulation of all 5*6 categories of second-order regular twisty puzzles. I imagine there will be over 1000 puzzles in total!
No comments:
Post a Comment